
Behind the pizza trick lies a powerful mathematical result about curved surfaces. Its discoverer, the mathematical genius Carl Friedrich Gauss, named it Theorema Egregium.

We’ve all been there. You pick up a slice of pizza and you’re about to take a bite, but it flops over and dangles limply from your fingers instead. The crust isn’t stiff enough to support the weight of the slice. Maybe you should have gone for fewer toppings. But there’s no need to despair, for years of pizza eating experience have taught you how to deal with this situation. Just fold the pizza slice into a U shape (aka the fold hold). This keeps the slice from flopping over, and you can proceed to enjoy your meal. (If you don’t have a slice of pizza handy, you can try this out with a sheet of paper.)

Behind this pizza trick lies a powerful mathematical result about curved surfaces, one that’s so startling that its discoverer, the mathematical genius Carl Friedrich Gauss, named it Theorema Egregium, Latin for excellent or remarkable theorem.
Take a sheet of paper and roll it into a cylinder. It might seem obvious that the paper is flat, while the cylinder is curved. But Gauss thought about this differently. He wanted to define the curvature of a surface in a way that doesn’t change when you bend the surface.
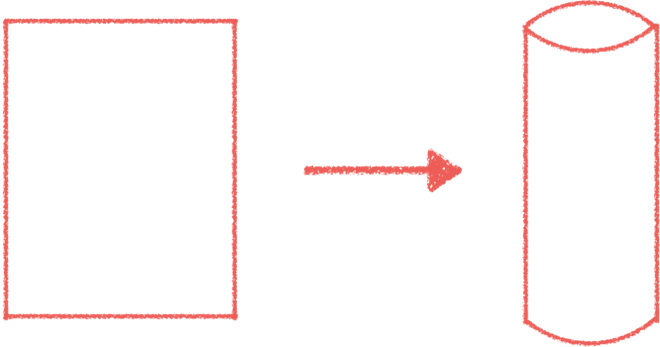
If you zoom in on an ant that lives on the cylinder, there are many possible paths the ant could take. It could decide to walk down the curved path, tracing out a circle, or it could walk along the flat path, tracing out a straight line. Or it might do something in between, tracing out a helix.
Gauss’s brilliant insight was to define the curvature of a surface in a way that takes all these choices into account. Here’s how it works. Starting at any point, find the two most extreme paths that an ant can choose (i.e. the most concave path and the most convex path). Then multiply the curvature of those paths together (curvature is positive for concave paths, zero for flat paths, and negative for convex paths). And, voila, the number you get is Gauss’s definition of the curvature at that point.

Let’s try some examples. For the ant on the cylinder, the two extreme paths available to it are the curved, circle-shaped path, and the flat, straight-line path. But since the flat path has zero curvature, when you multiply the two curvatures together you get zero. As mathematicians would say, a cylinder is flat – it has zero Gaussian curvature. Which reflects the fact that you can roll one out of a sheet of paper.
If, instead, the ant lived on a ball, there would be no flat paths available to it. Now every path curves by the same amount, and so the Gaussian curvature is some positive number. So spheres are curved while cylinders are flat. You can bend a sheet of paper into a tube, but you can never bend it into a ball.

Gauss’s remarkable theorem, the one which I like to imagine made him giggle with joy, is that an ant living on a surface can work out its curvature without ever having to step outside the surface, just by measuring distances and doing some math. This, by the way, is what allows us to determine whether our universe is curved without ever having to step outside of the universe (as far as we can tell, it’s flat).
A surprising consequence of this result is that you can take a surface and bend it any way you like, so long as you don’t stretch, shrink or tear it, and the Gaussian curvature stays the same. That’s because bending doesn’t change any distances on the surface, and so the ant living on the surface would still calculate the same Gaussian curvature as before.
This might sound a little abstract, but it has real-life consequences. Cut an orange in half, eat the insides (yum), then place the dome-shaped peel on the ground and stomp on it. The peel will never flatten out into a circle. Instead, it’ll tear itself apart. That’s because a sphere and a flat surface have different Gaussian curvatures, so there’s no way to flatten a sphere without distorting or tearing it. Ever tried gift wrapping a basketball? Same problem. No matter how you bend a sheet of paper, it’ll always retain a trace of its original flatness, so you end up with a crinkled mess.

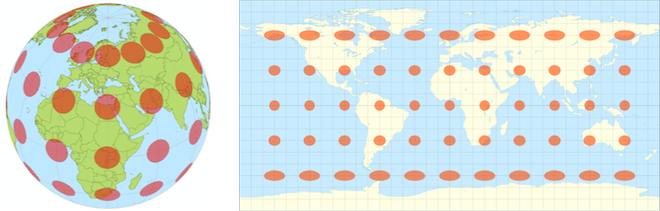
Another consequence of Gauss’s theorem is that it’s impossible to accurately depict a map on paper. The map of the world that you’re used to seeing depicts angles correctly, but it grossly distorts areas. The Museum of Math points out that clothing designers have a similar challenge – they design patterns on a flat surface that have to fit our curved bodies.
What does any of this have to do with pizza? Well, the pizza slice was flat before you picked it up (in math speak, it has zero Gaussian curvature). Gauss’s remarkable theorem assures us that one direction of the slice must always remain flat – no matter how you bend it, the pizza must retain a trace of its original flatness. When the slice flops over, the flat direction (shown in red below) is pointed sideways, which isn’t helpful for eating it. But by folding the pizza slice sideways, you’re forcing it to become flat in the other direction – the one that points towards your mouth. Theorema egregium, indeed.

By curving a sheet in one direction, you force it to become stiff in the other direction. Once you recognise this idea, you start seeing it everywhere. Look closely at a blade of grass. It’s often folded along its central vein, which adds stiffness and prevents it from flopping over. Engineers frequently use curvature to add strength to structures. In the Zarzuela race track in Madrid, the Spanish structural engineer Eduardo Torroja designed an innovative concrete roof that stretches out from the stadium, covering a large area while remaining just a few inches thick. It’s the pizza trick in disguise.

Curvature creates strength. Think about this: you can stand on an empty soda can, and it’ll easily carry your weight. Yet the wall of this can is just a few thousandths of an inch thick, or about as thick as a sheet of paper. The secret to a soda can’s incredible stiffness is its curvature. You can demonstrate this dramatically if someone pokes the can with a pencil while you’re standing on it. With even just a tiny dent, it’ll catastrophically buckle under your weight.

Perhaps the most mundane example of strength through curvature are the ubiquitous corrugated building materials (corrugate comes from ruga, Latin for wrinkle). You could hardly get more bland than a corrugated cardboard box. Tear one of these boxes apart, and you’ll find a familiar, undulating wave of cardboard inside the walls. The wrinkles aren’t there for any aesthetic reasons. They’re an ingenious way to keep a material thin and lightweight, yet stiff enough to resist bending under considerable loads.

Corrugated metal sheets use the same idea. These humble, unpretentious materials are a manifestation of pure utility, their form perfectly matched with their function. Their high strength and relatively low cost has blended them into the background of our modern world.
Today, we hardly give these wrinkled sheets of metal a second thought. But when it was first introduced, many saw corrugated iron as a wonder material. It was patented in 1829 by Henry Palmer, an English engineer in charge of the construction of the London Docks. Palmer built the world’s first corrugated iron structure, the Turpentine Shed at the London Docks, and although it might not seem remarkable to modern eyes, just listen to how an an architectural magazine of the time described it.
“On passing through the London Docks a short time ago, we were much gratified in meeting with a practical application of Mr Palmer’s newly invented roofing. […] **Every observing person, on passing by it, cannot fail being struck (considering it as a shed) with its elegance and simplicity, and a little reflection will, we think, convince them of its effectiveness and economy. It is, we should think, the lightest and strongest roof (for its weight), that has been constructed by man, since the time of Adam.** The total thickness of this said roof, appeared to us from a close inspection (and we climbed over sundry casks of sticky turpentine for that purpose,) to be, certainly not more, than a tenth of an inch!” [1]
They just don’t write architectural magazines like they used to.
While corrugated materials and soda cans are pretty strong, there’s a way to make materials even stronger. To discover it for yourself, go to your fridge and take out an egg. Put it in the palm of your hand, wrap your fingers around the egg, and squeeze. (Make sure you aren’t wearing a ring if you attempt this.) You’ll be amazed at its strength. I wasn’t able to crush the egg, and I gave it everything I had. (Seriously, you need to try this to believe it.)

What makes eggs so strong? Well, soda cans and corrugated metal sheets are curved in one direction but flat in the other. This curvature buys them some stiffness, but they can still potentially be flattened out into the flat sheets that they came from.
In contrast, egg shells are curved in both directions. This is the key to an egg’s strength. Expressed in math terms, these doubly curved surface have non-zero Gaussian curvature. Like the orange peel we encountered earlier, this means that they can never be flattened without tearing or stretching – Gauss’s theorem assures us of this fact. To crack an egg open, you first need to dent it. When the egg loses its curvature, it loses its strength.

The iconic shape for a nuclear power plant cooling tower also incorporates curvature in both directions. This shape, called a hyperboloid, minimizes the amount of material required to build it. Regular chimneys are a lot like giant soda cans – they’re strong, but they can also buckle easily. A hyperboloid shaped chimney solves this problem by curving in both directions. This double curvature locks the shape into place, giving it extra rigidity that a regular chimney lacks.
Another shape that gets its strength from double curvature is the Pringles potato chip*, or as mathematicians tend to call it, a hyperbolic paraboloid (say that three times fast).
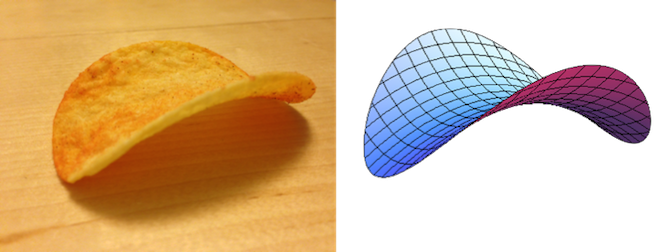
Nature exploits the strength of this shape in a mind-blowingly impressive way. The mantis shrimp is infamous for having one of the fastest punches in the animal kingdom, a punch so strong that it vaporises water, creating a shock wave and a flash of light. To deliver its impressive death blow, the mantis shrimp uses a hyperbolic paraboloid shaped spring. It compresses this spring to store up this immense energy, which it releases in one lethal blow.
You can watch biologist Sheila Patek describe her discovery of this amazing phenomenon. Or have Destin explain it to you in his brilliant Youtube channel Smarter Every Day.
The strength of this Pringles shape was well understood by the Spanish-Mexican architect and engineer Félix Candela. Candela was one of Eduardo Torroja’s students, and he built structures that took the hyperbolic paraboloid to new heights (literally). When you hear the word concrete, you might think of dreary, boxy constructions. Yet Candela was able to use the hyperbolic paraboloid shape to build huge structures that expressed the incredible thinness that concrete can provide. A true master of his medium, he was equal parts an innovative builder and a structural artist. His lightweight, graceful structures might seem delicate, but in fact they’re immensely strong and built to last.

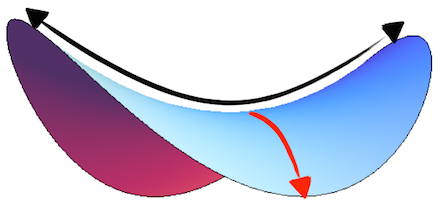
So what makes this Pringles shape so strong? It has to do with how it balances pushes and pulls. All structures have to support weight, and ultimately transfer this weight down to the ground. They can do this in two different ways. There’s compression, where the weight squeezes an object by pushing inwards. An arch is an example of a structure that exists in pure compression. And then there’s tension, where the weight pulls at the ends of an object, stretching it apart. Dangle a chain from its ends, and every part of it will be in pure tension. The hyperbolic paraboloid combines the best of both worlds. The concave U-shaped part is stretched in tension (shown in black) while the convex arch-shaped part is squeezed in compression (shown in red). Through double curvature, this shape strikes a delicate balance between these push and pull forces, allowing it to remain thin yet surprisingly strong.
Strength through curvature is an idea that shapes our world, and it has its roots in geometry. So the next time that you grab a slice, take a moment to look around, and appreciate the vast legacy behind this simple pizza trick.
Aatish Bhatia is a science writer, physicist, and science educator. Read the original article.

