
A detail of an Aeonium tabuliforme plant from Gothenburg, Sweden, displaying a Fibonacci spiral pattern. Photo: Max Ronnersjö/Wikimedia Commons, CC BY-SA 3.0
- Many indocentric claims about the Fibonacci series and the ‘golden ratio’ in mathematics don’t do justice to the actual history of the subject.
- It is easy these days to find articles and social media posts claiming to analyse the relationship between the Fibonacci series and golden ratio, and thereon to Indian culture.
- More often than not, such claims are used to float deceptive conclusions about how ancient Indian scholars knew these concepts and their applications.
Many indocentric claims about the Fibonacci series and the ‘golden ratio’ in mathematics don’t do justice to the actual history of the subject – while the proponents of these claims almost always exaggerate their assertions to a point where many original innovators don’t get their due credit.
The Fibonacci series is one of many interesting topics in mathematics, most importantly for its association with the golden ratio, which has a lot of peculiar properties and an equal number of myths related to it. You can obtain the Fibonacci series by taking two initial numbers, say 0 and 1, and then calculating the next term by adding the two previous terms. So the series goes thus:
0, 1, 1, 2, 3, 5, 8, 13, 21, …
The Fibonacci series also occurs throughout nature, like in the arrangement of certain seed patterns.
Through this article, let’s examine some historical arguments associated with the Fibonacci series, the golden ratio and their relationship – and to claims about work on these concepts by scholars in ancient India.
A line is said to be divided in the golden ratio if the ratio of the larger to the smaller part is as the whole to the larger part. As simple as it may sound, the implications of such a definition are profound. One is the self-similarity property of the golden ratio. This is obvious if you take the ‘golden rectangle’ (image below) and divide it according to the golden ratio. The part of the rectangle that remains will itself have sides whose lengths are proportionate to the golden ratio.
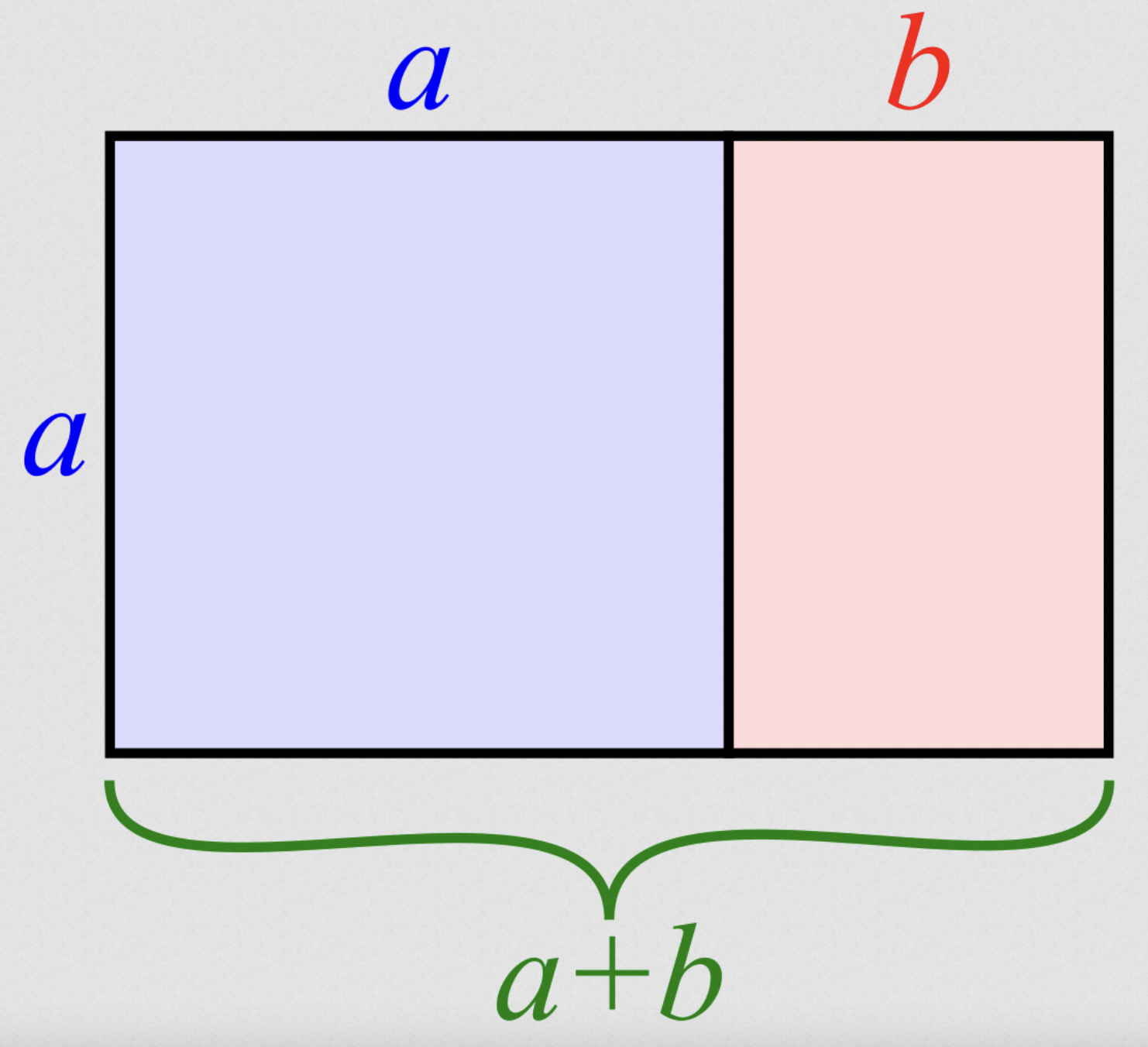
And if you continued this process of division as above, you will obtain a series of ever smaller rectangles whose sides are according to the golden ratio itself.
As the 17th century German astronomer Johannes Kepler wrote:
A peculiarity of this proportion lies in the fact that a similar proportion can be constructed out of the larger part and the whole; what was formerly the larger part now becomes the smaller, what was formerly the whole now becomes the larger part, and the sum of these two now has the ratio of the whole. This goes on indefinitely; the divine proportion always remaining…
The next interesting point is the relationship between the Fibonacci series and the golden ratio. Specifically, the ratio of consecutive terms of the series converges to the golden ratio as the number of terms are increased. For a substantial part of the history of the Fibonacci series, mathematicians didn’t recognise this relationship.
It is easy these days to find articles and social media posts claiming to analyse the relationship between the Fibonacci series and golden ratio, and thereon to Indian culture. More often than not, such claims are used to float deceptive conclusions about how ancient Indian scholars knew these concepts and their applications – at the same time without ever discussing these scholars’ work.
Most of these claims spiral out from one established fact that Sanskrit scholars, led by Pingala (c. second century BC), investigated a series that later came to be called the ‘Fibonacci series’, with reference to Sanskrit prosody[footnote]The pattern of sounds in a language or its poems.[/footnote]. The claimants here typically make four mistakes:
1. The Fibonacci series and the golden ratio are not the same thing, and for centuries mathematicians didn’t know about how they were related.
2. Some have said Fibonacci (a.k.a. Leonardo of Pisa) credited ancient Hindu scholars for the series named after him. However, Fibonacci appreciated the Hindu algorithms in his famous work on computations, Liber Abaci (1202), but didn’t credit the series to anyone. His approach also seems original and significantly different from the one Pingala employed.
3. Fibonacci himself didn’t know about the relationship between the series named after him and the golden ratio, although he worked with both of them. This relationship came to light in 1560, in the work of the German mathematician Simon Jacob, and followed by Kepler’s independent discovery in 1608.
4. Hindu scholars didn’t record the appearance of the golden ratio and the Fibonacci series in nature. These breakthroughs came later in medieval and modern Europe.
Also read: Madhava and the Uninfluential Discovery of Calculus

It’s important to repeat that the principal misconception among pro-Hindu propagandists today is that the series and the ratio are the same. They share a strong relationship, but our knowledge of them and their properties followed two distinct trajectories through history for a long time. This in turn quickly renders claims that “we always knew of the ratio” questionable.
The golden ratio is a fundamentally geometric concept initially investigated by the Greeks, starting with Euclid in his Elements, specifically in Book II, Proposition 11. Book VI of Elements deals with “a straight line cut in extreme and mean ratio” and deals with the ratio more clearly. Euclid’s definition goes thus: “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser” – which is precisely the golden ratio.
Euclid used the golden ratio to construct pentagons (Book IV) and certain platonic solids, such as the icosahedron and the dodecahedron (Book XIII). The sides and diagonals of these 2D and 3D shapes have the golden ratio baked into them.
Ancient Hindu scholars didn’t discuss the ratio at all – a fact made less surprising by the fact that they weren’t nearly as passionate as their Yavana counterparts in studying mathematics for its own sake; instead, they investigated ideas in mathematics for their applications, principally in computational astronomy. This isn’t to say we never did appreciate the natural beauty of the subject but only that such discussions appear sporadically through the literature.
The only evidence – and highly speculative, to wit – in favour of the knowledge of the golden ratio among Hindus comes in the work of Bhaskara II in the 12th century AD, where he describes the rules to construct a pentagon, without proof and without any explicit references to the value of the ratio or its definition.[footnote]Gupta, R., 1976, ‘Sine of eighteen degrees in India up to the eighteenth century’, Indian Journal of History of Science.[/footnote]
The next episode in the history of the golden ratio and the series happened with none other than Fibonacci. His investigations into the golden ratio in his book Practica Geometriae were purely of a geometric nature, in line with Euclidean geometry. Fibonacci presented multiple methods to calculate the lengths of sides of pentagons, decagons and so forth. But the series that he is most famous for, since called the Fibonacci series, appears in his Liber Abaci, which is dedicated to arithmetic.
In its pages, Fibonacci praises Hindu scholars for their ingenious algorithms, “including nine figures and zero”. Note that Fibonacci’s acclaim here is reserved for the Hindu decimal place value system and the associated algorithms. In the second half of Liber Abaci, Fibonacci provides several demonstrative examples of the use of this system in mathematics – one of which was the Fibonacci series. Together with his approach to develop the series, there is no discernible evidence that Fibonacci was familiar with the Sanskrit works of Pingala and his successors.
Equally importantly, neither Pingala nor any of the ancient scholars of the time knew of the golden ratio, and Fibonacci, while thoroughly familiar with the golden section, didn’t connect it with the series named for him.
In fact, in 1509, Luca Pacioli had composed a book about the golden section, entitled Divina Proportione. The text was illustrated by Leonardo da Vinci and included problems on Platonic solids. Pacioli describes several reasons as to why the golden ratio alone, among different ratios of interest, should be named the “divine proportion”. (Most of the other ratios were theological in nature.) Yet even he couldn’t spot the connection between the Fibonacci series and the ratio.
Also read: Bad Medicine, Fake History, Postcolonial Complicity – Ayurveda in the Time of COVID
That finding came in 1560, in a book by Simon Jacob. Kepler rediscovered this fact independently in 1608, in a letter addressed to a professor in Leipzig. So the much awaited communion of the Fibonacci series and the golden ratio happened in medieval Europe. Kepler also intuited the existence of the golden ratio and the Fibonacci number in leaf and flower patterns. As he wrote in 1611:
It is in the likeness of this self-developing series [referring to the recursive property of the Fibonacci sequence] that the faculty of propagation is, in my opinion, formed; and so in a flower the authentic flag of this faculty is shown, the pentagon.
A number of other scientists continued these studies of phyllotaxis – the arrangements of leaves and petals – and subsequently discovered many more examples of the occurrence of these concepts in the natural universe.
This is why we must be careful about ascribing these and similar achievements to ancient Hindu scholars – or even to temple-builders in India after the 10th century AD who worked the ratio into ‘divine architecture’. These are all highly speculative claims given the vast corpus of Hindu mathematical literature doesn’t discuss the corresponding mathematical concepts at all.
In sum, while ancient Hindu scholars knew of the existence of the series later named for Fibonacci, neither they nor many thinkers for centuries after knew about its relationship with the golden ratio. Second, there is no evidence that Fibonacci was aware of the work of Pingala or those who followed him or that Fibonacci copied from them; instead, his work, and those of his peers, was founded on different contexts, probing very different problems.
Every culture has made its fair share of contributions to the development of major human endeavours, including mathematics. The Egyptians who laid the ground for the earliest investigations of geometry, the Babylonians invented the place value system, the Greeks perfected the art of geometry and mathematical astronomy, and the Hindus devised the decimal system that has has come to be accepted as the standard arithmetic system around the world.
But to attribute everything to just one people in the name of cultural pride does no justice – either to the grandeur of the subject or the countless scholars who laboured to erect the mathematical ideas we work with today.
Sooraj (pseudonym) has an amateur interest in the history of science and mathematics and tweets at @r_montanus.

