Image: Shubham Dhage
- The principle of unitarity states that quantum information can’t be destroyed – yet that’s what black holes appear to do when they evaporate. Why the paradox?
- In the last few years, two potential resolutions have emerged, called entanglement islands and the holography of information.
- Both of their stories involve the work of Stephen Hawking, a major theoretical advance called the AdS/CFT correspondence and questions about quantum gravity.
- The papers behind the two resolutions have made pioneering contributions to physics, yet one of the resolutions has received more follow-up and coverage than the other.
The black hole information loss paradox has mystified and divided physicists for 40 years, but that may well be coming to an end. Hopes of an imminent solution have never been higher – even as opinions remain divided.
The paradox has the flavour of a magic trick. We’ve all seen the illusion where a magician hides an object behind a sheet and then removes it to reveal that the object has vanished. Black holes play a similar trick. First, they hide the information about things that have fallen inside. Then the black holes themselves disappear – through a gradual but unstoppable process of evaporation – apparently rendering all the information inside lost as well.
Just as the magician’s trick apparently violates the laws of physics, the black hole’s disappearing act seems to violate the rules of quantum theory. For physicists, figuring out what happens to the information has been a decades-long mystery. And we may finally be close to an answer.
This recent optimism stems from a discovery made three years ago, of an elusive phenomenon and its potential to resolve the paradox. This phenomenon, called entanglement islands, appears to show that information is not lost – that it does manage to make its way out of black holes.
At the time of the discovery, many physicists were quickly convinced that entanglement islands would resolve the black hole information-loss paradox, and deliver deeper insights into the subtle ways of nature.
All that remained was to close a few gaps in the story.
But today, three years later, those gaps are yet to be convincingly sealed. A minority of physicists remained sceptical of the entanglement islands solution, and their work since also suggests that the gaps might be bigger than they seemed to be at first.
Depending on whom you talk to, these gaps are either mere technicalities or fatal weaknesses.
In a curious turn of events, a different resolution to the paradox has emerged as a serious contender, called the holography of information. This proposal pitches that the paradox can be resolved if we took a certain counterintuitive property of gravitation more seriously – a property that, according to its proponents, its rival has missed.
A story with two plots

Thou shalt not destroy quantum information.
This is the principle of unitarity. It’s one of the central commandments of quantum theory. With every object, quantum theory associates a mathematical object called its quantum state. The state is like a dossier on the object: by analysing it using the tools of mathematics, physicists can decipher all of the object’s physical properties.
Knowledge of the quantum state is called quantum information. And the principle of unitarity holds that nothing can destroy quantum information.
In 1976, the British physicist Stephen Hawking famously showed that black holes constantly emit radiation from their vicinity, just beyond their surface. The quanta of radiation – the quantum particles that constitute the radiation, which are mostly photons, the particles of light – are entangled with the black hole itself.
Entanglement is when two objects store quantum information together. Entangled objects are like the torn-out halves of a treasure map. You need both pieces to make sense of the map. Similarly, you need both the entangled objects to access the information they contain.
When each quantum particle escapes from the vicinity of a black hole, some quantum information remains trapped inside – because the particle and the black hole are entangled.
A useful way to ‘count’ how much information is left behind inside the black hole is to keep track of the radiation’s entanglement entropy. Entanglement entropy is a measure of entanglement: it measures how entangled two objects are – in this case the radiation and the black hole. Its value tells us the amount of quantum information stuck inside the black hole.
With more and more quanta being radiated by the black hole, more and more information gets left behind in the black hole, and the entanglement entropy grows steadily. Meanwhile, the black hole keeps shrinking in size because the radiation is also taking away energy from the black hole. Unless the trapped information finds a way to escape the black hole, the entanglement entropy will keep growing – until the black hole disappears entirely.
The trapped quantum information will then be lost, and the principle of unitarity will be broken.
That cannot be allowed.
So where does the quantum information go?
We can thank the physicist Don Page for formulating the information loss paradox in terms of entanglement entropy. The plot showing entanglement entropy on the y-axis and time on the x-axis is called the Page curve.
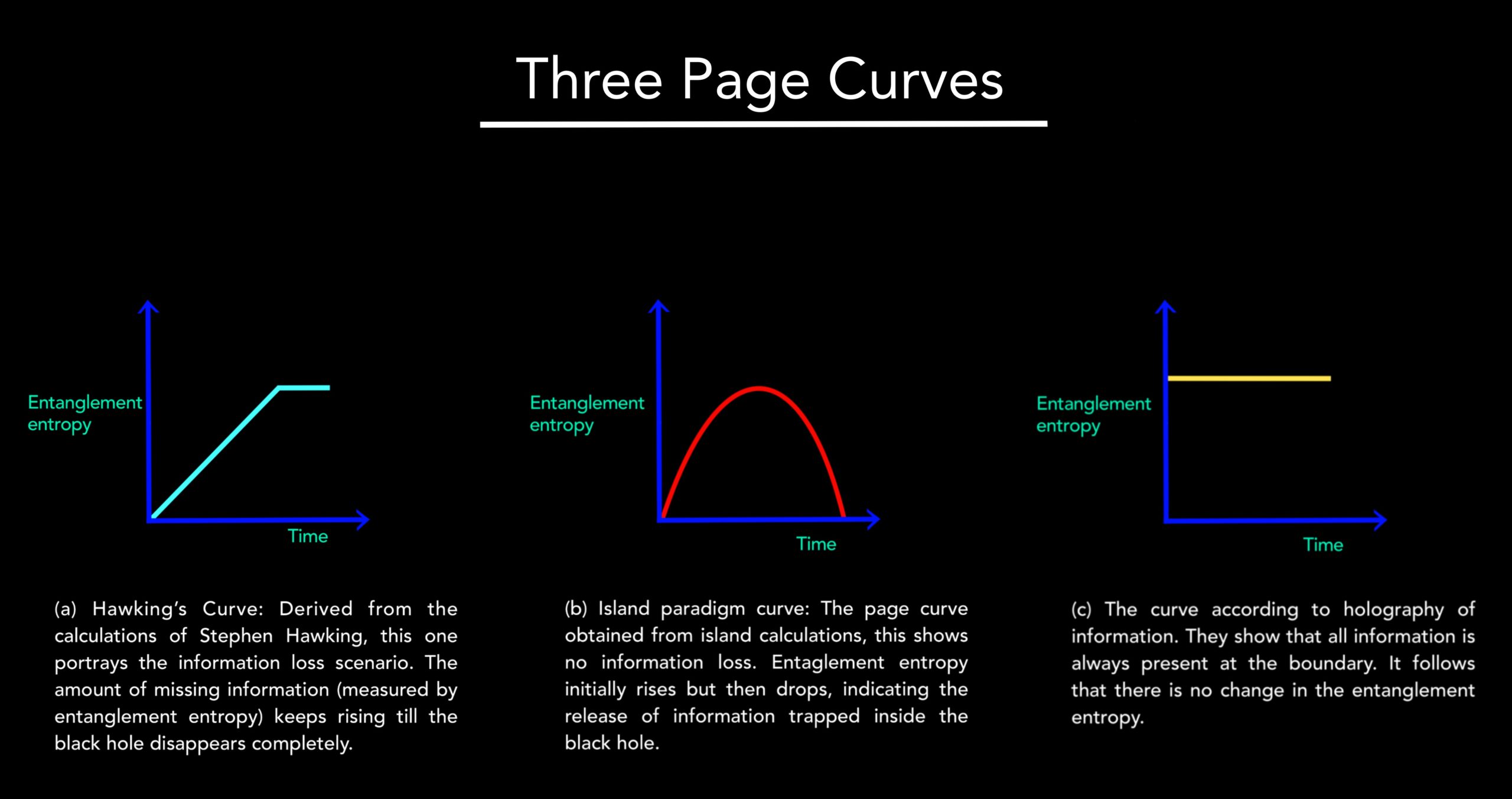
In 1993, Page showed that if physicists needed to save unitarity, the Page curve shouldn’t rise and then stop – as shown above – but climb back down as well. That is, the initial rise due to the entanglement piling up must be followed by an eventual downward turn, when the trapped information starts to leak out. When the entanglement entropy reaches zero, all the information will have leaked out.
This scenario is where it’s easiest to understand why the information loss paradox is so important. It’s an ideal natural laboratory where physicists can test the putative theories of quantum gravity – the elusive mathematical framework that neatly binds the laws of quantum physics with the laws of gravity.
While we’re likely many decades away from testing any theory of quantum gravity in an experiment, it will make a good case for itself if it can provide a clean resolution to the information loss paradox.
The holographic dictionary

Both proposals under discussion – the entanglement islands and the holography of information – owe their origins to the AdS/CFT correspondence, one of the biggest theoretical advances of our time.
The AdS/CFT correspondence proposes that there is a complete dictionary that allows physicists to translate between two apparently disparate theories. These theories operate in different dimensions.
One theory lives in a kind of spacetime called anti-de Sitter space (also called AdS), which is negatively curved everywhere and has a boundary on all sides. The anti-de Sitter space looks somewhat like a cylinder, and its outer surface is called the AdS boundary.
Say there’s an anti-de Sitter space in N dimensions and that there’s a theory of quantum gravity describing the physics in this universe. The boundary of the space will have N – 1 dimensions.
On this boundary lives another theory. It belongs to a special class of theories called conformal field theories.
The Argentine physicist Juan Maldacena proposed in 1997 that the physics of the N-dimensional anti-de Sitter universe is equivalent to the N – 1 dimensional conformal field theory living on its boundary. This is called the AdS/CFT correspondence. Although the correspondence is yet to be mathematically proven, there is a large body of mathematical evidence supporting it.
In an amusing analogy that physicists sometimes use – by reading the ingredients on the surface of the can, you get to know what’s inside.
AdS/CFT correspondence isn’t too different. Using the rules of the conformal field theory on the boundary surface of an anti-de Sitter space, physicists should be able to use the AdS/CFT correspondence to work out the rules of quantum gravity inside the anti-de Sitter universe itself.
The universe we live in is not an anti-de Sitter space. Our universe is a de Sitter space: it’s positively curved everywhere, expanding and has no boundaries. But we expect certain lessons about quantum gravity in an AdS universe to carry through.
Also, a caveat: while physicists believe the two theories in the two universes to be equivalent, they still don’t fully know how to translate between them. The AdS/CFT dictionary is a work in progress – physicists are still making new entries and updating old ones.
The dictionary entry that matters to the information loss paradox involves a way to describe entanglement entropy using a conformal field theory (CFT).
The Japanese physicists Shinsei Ryu and Tadashi Takayanagi first worked it out in 2006. Their entry tells us how to use the AdS/CFT correspondence to calculate the entanglement entropy in the CFT universe by measuring the area of a certain surface in the corresponding higher-dimensional anti-de Sitter universe.
Many intriguing results came out of the Ryu-Takayanagi proposal. One striking result is that every region in the CFT also has a twin region in the anti-de Sitter universe. The latter is called an entanglement wedge.
All quantum information present in the wedge is automatically present in the CFT region as well, even if they’re technically in separate universes.
The study of entanglement entropy and entanglement wedges has progressed steadily in the last decade, as physicists have fine-tuned the entanglement entropy formula.
The recent work on black hole information loss was a culmination of this progress – with one formula discovered by Aron Wall and Netta Engelhardt in 2018 playing a starring role.
The island

Two separate papers first proposed the entanglement-island solution in 2019. One was coauthored by Ahmed Almheiri, Netta Engelhardt, Don Marolf and Henry Maxfield; the other was authored by Geoff Penington.
Both papers considered a big black hole sitting in an anti-de Sitter universe. This black hole simply doesn’t evaporate. The boundary of its bounded spacetime reflects its radiation back, preventing energy loss from the universe.
The papers modified the boundary of the anti-de Sitter space to make it transparent to the radiation, allowing it to go through. They also added a thermal reservoir beyond the boundary. This way, the black hole could lose energy by radiating into the reservoir.
Now, each paper worked out the Page curve. But instead of following Hawking’s old calculation, they used the AdS/CFT dictionary – specifically, the Wall-Engelhardt formula.
They asked: how does the entanglement entropy of the reservoir, which collects the radiation, behave?
In the initial stages of the black hole’s evaporation, their answer matched what Hawking had found: the entanglement entropy rises steadily with time. But later they found that it decreased and went down to zero. So their calculation yielded not the rise-and-stop Page curve associated with the paradox but the rise-and-fall Page curve that saves unitarity!
How did this happen?
The picture emerging from the entanglement wedges was intriguing. The reservoir is in the anti-de Sitter space and has a corresponding entanglement wedge in a CFT space. At first, the wedge contains only the radiation from the black hole. But over time it grows such that there is a second wing in the anti-de Sitter space that envelopes the black hole. This second wing is called the entanglement island.
The implication is that all information in the island, including that trapped in the black hole, is transferred to the radiation in the reservoir. No information is lost. All of it is somehow encrypted into the radiation.
Two other papers – one by Penington, Stephen Shenker, Douglas Stanford and Zhenbin Yang and another by Ahmed Almheiri, Thomas Hartman, Maldacena, Edgar Shaghoulian and Amirhossein Tajdini – used a different tack but arrived at the same result.
All four papers together revealed where Hawking’s calculations had gone wrong: he had assumed that he could neglect the quantum effects on space and time itself.
Specifically, Hawking had gone by the conventional wisdom of the separation of scales: roughly that, while describing a phenomenon at one scale, he didn’t need to account for the laws of physics operating at much smaller scales. When computing the trajectory of a planet, for example, you can safely neglect the rules of atomic physics.
Hawking overlooked the quantum fluctuations of space and time. The island phenomenon appears to have its origins precisely in these fluctuations.
The island calculation remains the first instance of a full calculation – starting from the first principles of a theory of quantum gravity and ending with an answer, to show quantum information is not lost when black holes evaporate.
This is how this proposed resolution is very different from previous ones, which involved ad hoc modifications to known physics solely for the purpose of solving the paradox. Here, physicists simply asked what the AdS/CFT correspondence says about a black hole radiating into a reservoir and the answer led them to a result that saved unitarity.
Yet the black hole information loss paradox can’t be said to be fully resolved: we’re none the wiser about how the information was transferred from the black hole to the radiation. The computation only showed that all the information got out before the black hole finished evaporating.
Somehow, a black hole manages to encode the trapped information into the radiation and sets it free.
Islands critiqued

While the community of physicists quickly accepted the island paradigm, some of them also pointed out some loose ends. In particular, a few sceptics have argued that while the calculations are correct, they don’t help resolve the black hole information-loss paradox.
The troubles stem from the reservoir attached to the anti-de Sitter universe. The physicists who authored the island papers assumed that gravity stopped at the boundary of the anti-de Sitter space and didn’t enter the reservoir. This is not an innocuous assumption.
In a 2020 paper, Hao Geng and Andreas Karch showed that in more than two dimensions, stopping gravity dead at the edge of the reservoir would modify the theory of gravity. Specifically, the hypothetical carriers of the gravitational force – known as gravitons[footnote]Just like the carriers of the electromagnetic force are photons.[/footnote] – have no mass. The modification would give gravitons a tiny bit of mass. The island papers are therefore working not with general relativity but something else, which means it’s not quite solving the right problem.
Geng, Karch as well as Suvrat Raju, Lisa Randall, Carlos Perez-Pardavila, Sanjit Sashi and Marcos Riojas raised even more objections. In a 2021 paper, they considered a situation in which gravity does enter the reservoir – and found that the resulting Page curve doesn’t rise and fall. Instead, it’s just horizontal. The entanglement entropy stays constant.
Another of their papers raised a new concern. With some reasonable assumptions about quantum gravity, the authors could show that all the quantum information from the black hole could be accessed at the boundary of the anti-de Sitter space. This contradicts the result that some of the information gets sent to the reservoir, and shouldn’t be available at the boundary.
One way to resolve this glitch is to modify Einstein’s theory of gravity to make gravitons massive – which is exactly the modification that the island papers made.
The key takeaway is that the island way to recover information and save unitarity works perfectly well – if you slightly modify Einstein’s theory of gravity.
These criticisms have been around for some two years now, and physicists are yet to resolve them in print. At the same time, the physicists behind the island proposal also remain confident that their results will hold for Einsteinian gravity as well, that the objections are either minor technicalities or evadable with slight changes in their math.
This said, they haven’t undertaken an explicit calculation to prove their points.
So while the island paradigm appears close to the finish line of the race to solve the paradox, there is a slight possibility that they have actually run the wrong race.
But even if the critics are right and the island solution only works for theories in which gravitons have mass, the discovery of islands, their relationship with quantum effects on spacetime and the breakdown of the separation of scales are pioneering contributions to the study of quantum gravity.
Holography of information

As it happens, some of these criticisms of the island paradigm are closely related to the ideas behind the ‘holography of information’ programme. First formulated by Suvrat Raju and developed by Raju, Alok Laddha, Siddharth Prabhu and Pushkal Shrivastava in a series of papers, it contends that the black hole information-loss paradox goes away if we take gravity more seriously.
That is, in this view, both the island proposal as well as Hawking made the same mistake that Wile E. Coyote did: they failed to take gravity into account.
Raju is currently at the International Centre for Theoretical Sciences, Bengaluru.
The central insight of ‘holography of information’ is that gravity plays an important role in how the universe stores information. Earlier work had followed the wisdom of scale-separation and neglected the effects of gravity. The potential quantum effects of gravity allow for radically different results.
This difference is captured in an omission that Stephen Hawking made when he derived the black hole information-loss paradox. He assumed that quantum information inside a black hole wouldn’t be detectable from the outside.
That is, he assumed that the split property holds. It doesn’t.
Raju showed in an October 2021 paper that quantum gravity violates the split property. Specifically, the quantum effects of gravity ensure that information is hoarded at the boundary of the universe.
(‘Holography’ is derived from the Greek holos and grapho, meaning ‘whole’ and ‘to scratch’. Holography of information thus denotes the ability to access all the information by studying the surface.)
For example, say there’s a closed box in front of you and you’re wondering what could be inside. It might seem like there’s no way to know unless you can open the box and check. But this is not true.
By combining the principles of quantum theory and gravity, together with some mild assumptions about some unknown aspects of quantum gravity, Raju and his collaborators concluded that the boundary of the universe ‘sees’ everything – that is, all the quantum information in the universe is recorded at its boundary at all times. You can deduce the contents of the box in front of you by making measurements on the boundary of the universe.
This is a different kind of resolution to the paradox: that no quantum information was ever missing to begin with, that instead, it was always on the universe’s boundary! The entanglement entropy neither rises nor falls; the Page curve is an unwavering horizontal line.
Setting aside whether this approach is the correct resolution, the results of Raju & co. about the split property no longer holding and about gravity stacking information at the spacetime boundary are important contributions that are likely to be a part of any complete story of black holes and information loss.
The community’s reaction to this proposal has been mixed, however. Everyone agrees that the results are technically correct – but they aren’t agreed about the right way to interpret them. A popular opinion among supporters of the island idea is that the island computation only tracked the information trapped inside the black hole, which increased initially and then decreased as the black hole’s information became available outside. On the other hand, the holography of information computations tracked the information of the black hole and the radiation taken together, which is never lost.
At the heart of this debate is a question: while all information about the universe’s interior is at its boundary, can one distinguish between quantum information about the black hole from quantum information about the radiation? Some think this should be possible; the ‘holography of information’ folks disagree. We don’t have the final word yet.
A sociological paradox

In terms of impact on the physics community, the island papers are among the greatest in the last decade. Within months of their publication, work on the paradox blew up. But the questions that critics have raised – even though they’ve been around for two years now – have received very little follow-up, and the ‘holography of information’ programme even less.
In fact, we have a slightly lopsided situation today: physicists continue to publish papers by the hundreds about the entanglement islands but few attempt to answer whether the islands are compatible with the Einsteinian gravity of our universe.
Media attention on the topics has been similarly disproportionate. The island idea has received extensive coverage while the criticism and the holography proposal have stayed mostly out of sight.
I believe the reasons behind this have to do not only with physics but also sociology.
The fact that the work on islands largely originated in institutions like the universities of Princeton and Stanford likely influenced how both the media and the community of physicists have received it.
The enormous pressure on scientists to publish papers on topics that are ‘fashionable’ determines which problems physicists choose to work on in the first place. Choosing the essentially formula-plugging, and often conceptually unenlightening, projects that the topic of entanglement islands currently offers is a much safer bet to get ahead in the ‘publications or perish’ race than tackling open questions about loopholes in the proposal – even though the latter is more important for progress.
Whether physicists can make the island proposal work with Einsteinian gravity deserves some attention – as does the tension between the island proposal and the holography of information. Both sides are clearly getting certain things right. It’s up to the community now to untangle the true from the false, and get closer to solving the mystery of black hole information loss once and for all.
It would seem there’s never been a more exciting time to be in the black hole information loss business.
Note: The list of authors of a 2021 paper critiquing the islands idea was updated at 6:47 am on November 14, 2022, to include Marcos Riojas.
Nirmalya Kajuri is an assistant professor of physics in IIT Mandi.


